dkolomenskiy

Dmitry Kolomenskiy

Assistant Professor
Center for Materials Technologies

Dr. Dmitry Kolomenskiy is a specialist in fluid mechanics. He received his Ph.D. degree from the University of Aix-Marseille (France), and held academic positions at universities and research institutes in France, Canada and Japan, prior to joining Skoltech. Dr. Kolomenskiy was a postdoctoral fellow at CERFACS (France), McGill University (Canada), Chiba University (Japan), a project scientist at JAMSTEC (Japan), and a specially appointed associate professor at Tokyo Institute of Technology (Japan). In addition, he held visiting fellowships at DAMTP, University of Cambridge (UK), and ESPCI Paris (France). His research concerns mainly with computational fluid dynamics and fluid-solid interaction. His research topics encompass the biolocomotion, vortex dynamics, fluid-solid interaction, and high-performance computing. He develops mathematical models ranging from reduced-order analytical description to direct numerical simulation, on the interface between engineering and biological sciences. He contributed to the development of computational fluid dynamics approaches such as volume penalization and wavelet-based adaptive methods. Besides the work related with the biomechanics, he has been involved in interdisciplinary international collaborative projects with marine biologists, aeronautical engineers, and environmental scientists. His research at Skoltech focuses on the computational fluid dynamics in application to the development of new design and manufacturing processes at CMT.

 

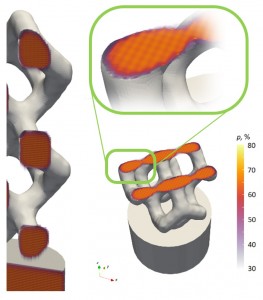
Numerical simulation of 3D printing from ceramic pastesCeramic 3D printing is a rapidly developing area of additive manufacturing technologies. When a piece of ceramics is manufactured, it goes through a multi-stage technological process. The geometrical shape of the product needs to remain under control through all stages, as well as the mechanical properties. We focus on the stereolithographic technology, where ceramic particles are diluted into chemical monomers that convert into polymers under laser treatment. Three-dimensional solid parts are grown in a layer by layer fashion. In this ongoing project, we attempt to better understand the limitations, typical defects of this process, and to develop a predictive model that would allow to achieve the best geometrical and mechanical properties of ceramic parts produced by stereolithography. Numerical simulation of 3D printing from ceramic pastes

 

3D printing from shape memory polymersShape memory polymers (SMP) can change geometric configuration in response to external stimuli. Our research focuses on the finite-element modelling of 3D-printed SMP parts. In order to capture the shape memory effect of thermally activated polymers, we apply multi-branch constitutive models having two distinct sets of non-equilibrium branches that represent the glassy mode of relaxation and the Rouse modes in the rubbery state. This model is time- and temperature-dependent and applicable for 4D-printing with the fourth dimension referring to time. 3D printing from shape memory polymers

 

Numerical simulation of spray coatingThe gas dynamic spray is a surface coating technique in which coating is formed by treatment of a metallic substrate by a high-velocity impinging particle-laden jet. This process generates a thin layer with a complex nanocrystalline structure in the impingement zone. Optimization of spraying systems continues evolving from an empirical trial and error process to a model-based approach by virtue of the improving completeness and predictive capacity of mathematical models. In this project with the Laboratory of Thermal Spray and Functional Coatings, we perform direct numerical simulation of the particle-laden flow to explore the effect of unsteady vortical structures and particle agglomeration in the impingement layer. 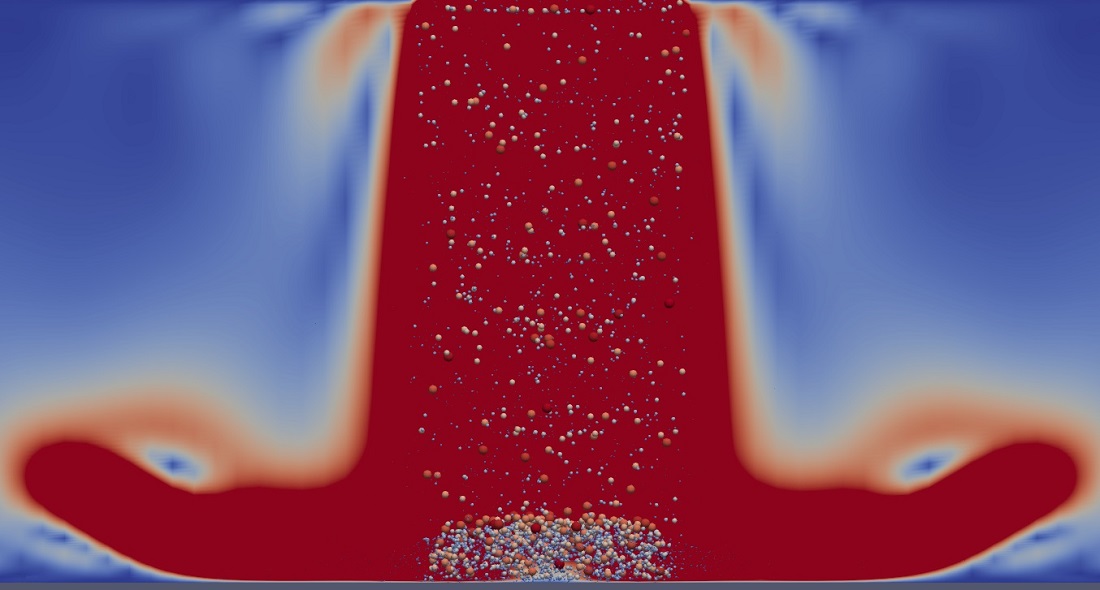Numerical simulation of spray coating

 

Biomechanics and biomimeticsMaterials and designs produced by additive manufacturing share similarities with the biological ones in the respect that they are grown by layers, which allows for a great variety of shapes and multi-component structures. Taking this standpoint, we explore the function of such materials and designs in living organisms, with a focus on mechanisms that enable locomotion in air and in water. Follow the links to learn more about the wings of tiny insects and swimming gaits of aquarium fish. 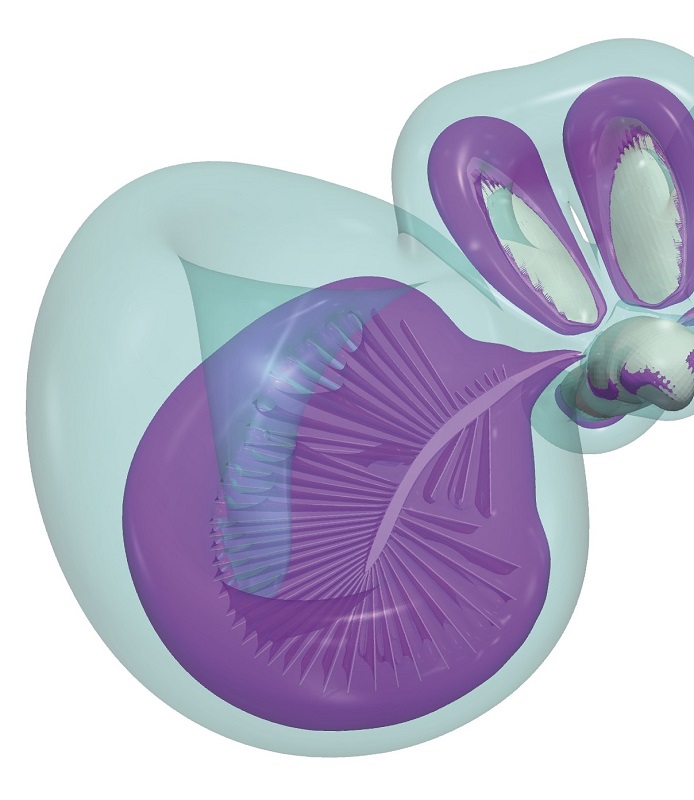Biomechanics and biomimetics
  1. D. Kolomenskiy. Recent progress in the biomechanics of flight of miniature insects with bristled wings. Journal of the Physical Society of Japan 92:121004, 2023. https://doi.org/10.7566/JPSJ.92.121004
  2. G. Li, L. Duan, J. Sesterhenn, R. Godoy-Diana, B. Thiria, D. Kolomenskiy. Far-field hydrodynamic interaction in a group of swimmers. Journal of Fluid Mechanics 974:A34, 2023. https://doi.org/10.1017/jfm.2023.802
  3. G. Li, D. Kolomenskiy, H. Liu, R. Godoy-Diana, B. Thiria. Intermittent versus continuous swimming: An optimization tale. Physical Review Fluids 8(1):013101, 2023. https://doi.org/10.1103/PhysRevFluids.8.013101
  4. M. Vulf, V. Petrov, A. Sulimov, A. Simonova, A. Kazak, S. Chugunov, D. Kolomenskiy. A novel droplet generator and a bench-testing rig enabling research on suspension droplet wall impingement and particle deposition. Coatings 13(1):129, 2023. https://doi.org/10.3390/coatings13010129
  5. R. Onishi, J. Hirai, D. Kolomenskiy, Y. Yasuda. Real-time high-resolution prediction of orographic rainfall for early warning of landslides.
    Progress in Landslide Research and Technology 1(1):237–248, 2022. https://doi.org/10.1007/978-3-031-16898-7_17
  6. S. E. Farisenkov, D. Kolomenskiy, P. N. Petrov, T. Engels, N. A. Lapina, F.-O. Lehmann, R. Onishi, H. Liu, A. A. Polilov. Novel flight style and light wings boost flight performance of tiny beetles. Nature 602:96-100, 2022. https://doi.org/10.1038/s41586-021-04303-7
  7. T. Engels, H. Truong, M. Farge, D. Kolomenskiy, K. Schneider. Computational aerodynamics of insect flight using volume penalization. Comptes Rendus. Mécanique, online first, 1–20, 2022. https://doi.org/10.5802/crmeca.129
  8. G. Li, D. Kolomenskiy, H. Liu, B. Thiria, R. Godoy-Diana. Hydrodynamical fingerprint of a neighbour in a fish lateral line. Frontiers in Robotics and AI 9:825889, 2022. https://doi.org/10.3389%2Ffrobt.2022.825889
  9. X. Cai, Y. Xue, D. Kolomenskiy, R. Xu, H. Liu. Elastic storage enables robustness of flapping wing dynamics. Bioinspiration & Biomimetics 17:045003, 2022. https://doi.org/10.1088/1748-3190/ac6c66
  10. D. Kolomenskiy, R. Onishi, H. Uehara. WaveRange: wavelet-based data compression for three-dimensional numerical simulations on regular grids. Journal of Visualization 25:543–573, 2022. https://doi.org/10.1007/s12650-021-00813-8
  11. H. Truong, T. Engels, H. Wehmann, D. Kolomenskiy, F.-O. Lehmann, K. Schneider. An experimental data-driven mass-spring model of flexible Calliphora wings, Bioinspiration & Biomimetics 17:026003, 2022. https://doi.org/10.1088/1748-3190/ac2f56
  12. Y. Yasuda, R. Onishi, Y. Hirokawa, D. Kolomenskiy, D. Sugiyama. Super-resolution of near-surface temperature utilizing physical quantities for real-time prediction of urban micrometeorology. Building and Environment 209:108597, 2022. https://doi.org/10.1016/j.buildenv.2021.108597
  13. T. Engels, D. Kolomenskiy, F.-O. Lehmann. Flight efficiency is a key to diverse wing morphologies in small insects. Journal of the Royal Society Interface, 18(183):20210518, 2021. https://doi.org/10.1098/rsif.2021.0518
  14. X. Cai, D. Kolomenskiy, T. Nakata, H. Liu. A CFD data-driven aerodynamic model for fast and precise prediction of flapping aerodynamics in various flight velocities. Journal of Fluid Mechanics 915:A114, 2021. https://doi.org/10.1017/jfm.2021.68
  15. G. Li, I. Ashraf, B. François, D. Kolomenskiy, F. Lechenault, R. Godoy-Diana, B. Thiria. Burst-and-coast swimmers optimize gait by adapting unique intrinsic cycle. Communications Biology 4:40, 2021. https://doi.org/10.1038/s42003-020-01521-z
  16. H. Truong, T. Engels, D. Kolomenskiy, K. Schneider. Influence of wing flexibility on the aerodynamic performance of a tethered flapping bumblebee. Theoretical and Applied Mechanics Letters 10:382-389, 2020. https://doi.org/10.1016/j.taml.2020.01.056
  17. D. Kolomenskiy, S. Farisenkov, T. Engels, N. Lapina, P. Petrov, F.-O. Lehmann, R. Onishi, H. Liu, A. Polilov. Aerodynamic performance of a bristled wing of a very small insect. Experiments in Fluids 61:194, 2020. https://doi.org/10.1007/s00348-020-03027-0
  18. H. Truong, T. Engels, D. Kolomenskiy, K. Schneider. A mass-spring fluid-structure interaction solver: Application to flexible revolving wings. Computers & Fluids 200:104426, 2020. https://doi.org/10.1016/j.compfluid.2020.104426
  19. S. Ravi, R. Noda, S. Gagliardi, D. Kolomenskiy, S. Combes, H. Liu, A. Biewener, N. Konow. Modulation of flight muscle recruitment and wing rotation enables hummingbirds to mitigate aerial roll perturbations. Current Biology 30:187-195, 2020. https://doi.org/10.1016/j.cub.2019.11.025
  20. G. Li, D. Kolomenskiy, H. Liu, B. Thiria, R. Godoy-Diana. On the energetics and stability of a minimal fish school. PLoS One 14(8):e0215265, 2019. https://doi.org/10.1371/journal.pone.0215265
  21. D. Kolomenskiy, S. Ravi, R. Xu, K. Ueyama, T. Jakobi, T. Engels, T. Nakata, J. Sesterhenn, M. Farge, K. Schneider, R. Onishi, H. Liu. Wing morphology and inertial properties of bumblebees. Journal of Aero Aqua Bio-mechanisms 8(1):41-47, 2019. https://doi.org/10.5226/jabmech.8.41
  22. G. Li, D. Kolomenskiy, H. Liu, B. Thiria, R. Godoy-Diana. On the interference of vorticity and pressure fields of a minimal fish school. Journal of Aero Aqua Bio-mechanisms 8(1):27-33, 2019. https://doi.org/10.5226/jabmech.8.27
  23. D. Kolomenskiy, S. Ravi, R. Xu, K. Ueyama, T. Jakobi, T. Engels, T. Nakata, J. Sesterhenn, K. Schneider, R. Onishi, H. Liu. The dynamics of passive feathering rotation in hovering flight of bumblebees. Journal of Fluids and Structures 91:102628, 2019. https://doi.org/10.1016/j.jfluidstructs.2019.03.021
  24. T. Engels, D. Kolomenskiy, K. Schneider, M. Farge, F.-O. Lehmann, J. Sesterhenn. Impact of turbulence on flying insects in tethered and free flight: high-resolution numerical experiments. Physical Review Fluids 4:013103, 2019. https://doi.org/10.1103/PhysRevFluids.4.013103
  25. D. Chen, D. Kolomenskiy, R. Onishi, H. Liu. Versatile reduced-order model of leading-edge vortices on rotary wings. Physical Review Fluids 3:114703, 2018. https://doi.org/10.1103/PhysRevFluids.3.114703
  26. T. Jakobi, D. Kolomenskiy, T. Ikeda, S. Watkins, A. Fisher, H. Liu, S. Ravi. Bees with attitude: the effects of directed gusts on flight trajectories. Biology Open 7:bio034074, 2018. https://doi.org/10.1242/bio.034074
  27. D. Kolomenskiy, R. Paoli. Numerical simulation of the wake of an airliner. Journal of Aircraft 55(4):1689-1699, 2018. https://doi.org/10.2514/1.C034349
  28. T. Engels, D. Kolomenskiy, K. Schneider, M. Farge, F.-O. Lehmann, J. Sesterhenn. Helical vortices generated by flapping wings of bumblebees. Fluid Dynamics Research 50(1):011419, 2018. https://doi.org/10.1088/1873-7005/aa908f
  29. D. Chen, D. Kolomenskiy, T. Nakata, H. Liu. Forewings match the formation of leading-edge vortices and dominate aerodynamic force production in revolving insect wings. Bioinspiration & Biomimetics 13(1):016009, 2018. https://doi.org/10.1088/1748-3190/aa94d7
  30. D. Chen, D. Kolomenskiy, H. Liu. Closed-form solution for the edge vortex of a revolving plate. Journal of Fluid Mechanics 821:200-218, 2017. https://doi.org/10.1017/jfm.2017.257
  31. H. Liu, D. Kolomenskiy, T. Nakata, G. Li. Unsteady bio-fluid dynamics in flying and swimming. Acta Mechanica Sinica 33(4):663-684, 2017. https://doi.org/10.1007/s10409-017-0677-4
  32. S. Ravi, D. Kolomenskiy, T. Engels, K. Schneider, C. Wang, J. Sesterhenn, H. Liu. Bumblebees minimize control challenges by combining active and passive modes in unsteady winds. Scientific Reports 6:35043, 2016. https://doi.org/10.1038/srep35043
  33. T. Engels, D. Kolomenskiy, K. Schneider, J. Sesterhenn. FluSI: a novel parallel simulation tool for flapping insect flight using a Fourier method with volume penalization. SIAM Journal on Scientific Computing 38(5):S3-S24, 2016. https://doi.org/10.1137/15M1026006
  34. H. Liu, S. Ravi, D. Kolomenskiy, H. Tanaka. Biomechanics and biomimetics in insect-inspired flight systems. Philosophical Transactions of the Royal Society B: Biological Sciences, 371(1704):20150390, 2016. https://doi.org/10.1098/rstb.2015.0390
  35. D. Kolomenskiy, M. Maeda, T. Engels, H. Liu, K. Schneider, J.-C. Nave. Aerodynamic ground effect in fruitfly sized insect takeoff. PLoS One 11(3):e0152072, 2016. https://doi.org/10.1371/journal.pone.0152072
  36. T. Engels, D. Kolomenskiy, K. Schneider, F.-O. Lehmann and J. Sesterhenn. Bumblebee flight in heavy turbulence. Physical Review Letters 116:028103, 2016. https://doi.org/10.1103/PhysRevLett.116.028103
  37. D. Kolomenskiy, J.-C. Nave, K. Schneider. Adaptive gradient-augmented level set method with multiresolution error estimation. Journal of Scientific Computing 66(1):116-140, 2016. https://doi.org/10.1007/s10915-015-0014-7
  38. T. Engels, D. Kolomenskiy, K. Schneider, J. Sesterhenn. Numerical simulation of fluid-structure interaction with the volume penalization method. Journal of Computational Physics 281:96-115, 2015. https://doi.org/10.1016/j.jcp.2014.10.005
  39. D. Kolomenskiy, R. Nguyen van yen, K. Schneider. Analysis and discretization of the volume penalized Laplace operator with Neumann boundary conditions. Applied Numerical Mathematics 95:238-249, 2015. https://doi.org/10.1016/j.apnum.2014.02.003
  40. R. Nguyen van yen, D. Kolomenskiy, K. Schneider. Approximation of the Laplace and Stokes operators with Dirichlet boundary conditions through volume penalization: a spectral viewpoint. Numerische Mathematik 128(2):301-338, 2014. https://doi.org/10.1007/s00211-014-0610-8
  41. D. Kolomenskiy, Y. Elimelech, K. Schneider. Leading-edge vortex shedding from rotating wings. Fluid Dynamics Research 46:031421, 2014. https://doi.org/10.1088/0169-5983/46/3/031421
  42. G. Bimbard, D. Kolomenskiy, J. Casas, R. Godoy-Diana. Large kinematic variability during take-off in butterflies due to varying relative timing of legs and aerodynamic forces. Journal of Experimental Biology 216:3551-3563, 2013. https://doi.org/10.1242/jeb.084699
  43. T. Engels, D. Kolomenskiy, K. Schneider, J. Sesterhenn. Numerical simulation of the fluttering instability using a pseudospectral method with volume penalization. Computers and Structures 122:101-112, 2013. https://doi.org/10.1016/j.compstruc.2012.12.007
  44. D. Kolomenskiy, H. K. Moffatt. Similarity solutions for unsteady stagnation point flow. Journal of Fluid Mechanics 711:394-410, 2012. https://doi.org/10.1017/jfm.2012.397
  45. B. Kadoch, D. Kolomenskiy, P. Angot, K. Schneider. A volume penalization method for incompressible flows and scalar advection-diffusion with moving obstacles. Journal of Computational Physics 231:4365-4383, 2012. https://doi.org/10.1016/j.jcp.2012.01.036
  46. D. Kolomenskiy, H. K. Moffatt, M. Farge, K. Schneider. Two- and three-dimensional numerical simulations of the clap-fling-sweep of hovering insects. Journal of Fluids and Structures 27(5-6):784-791, 2011. https://doi.org/10.1016/j.jfluidstructs.2011.05.00
  47. D. Kolomenskiy, H. K. Moffatt, M. Farge, K. Schneider. The Lighthill – Weis-Fogh clap-fling-sweep mechanism revisited. Journal of Fluid Mechanics 676:572-606, 2011. https://doi.org/10.1017/jfm.2011.83
  48. D. Kolomenskiy, K. Schneider. Numerical simulations of falling leaves using a pseudo-spectral method with volume penalization. Theoretical and Computational Fluid Dynamics 24(1-4):169-173, 2010. https://doi.org/10.1007/s00162-009-0171-0
  49. D. Kolomenskiy, H. K. Moffatt, M. Farge, K. Schneider. Vorticity generation during the clap-fling-sweep of some hovering insects. Theoretical and Computational Fluid Dynamics 24(1-4):209-215, 2010. https://doi.org/10.1007/s00162-009-0137-2
  50. D. Kolomenskiy, K. Schneider. A Fourier spectral method for the Navier-Stokes equations with volume penalization for moving solid obstacles. Journal of Computational Physics 228:5687-5709, 2009. https://doi.org/10.1016/j.jcp.2009.04.026
  51. R. Nguyen van yen, M. Farge, D. Kolomenskiy, K. Schneider, N. Kingsbury. Wavelets meet Burgulence: CVS-filtered Burgers equation. Physica D 237:2151-2157, 2008. https://doi.org/10.1016/j.physd.2008.02.011

09.11.2023

The next research seminar of the Center for Materials Technologies is scheduled for Wednesday, November 15, 11 AM.

Our speaker is Dr. Bernd R. Noack, Chair of Artificial Intelligence and Aerodynamics (CAIA), School of Mechanical Engineering and Automation, Harbin Institute of Technology, Shenzhen, China, with the topic “Taming turbulence with many actuators, many sensors and machine learning”.

The seminar will be held in hybrid mode.

Offline: E-R3-2007

Online: Join via https://vc.skoltech.ru/b/ann-ibj-zln-nxx

Announcement in pdf

announcement


kirillovbogdan
Bogdan Kirillov
Research Scientist
vilinskimazurkatherine
Katherine Vilinski-Mazur
Junior Research Scientist

Numerical Methods in Engineering and Applied Science (6 ECTS)

The course provides students with the understanding and working knowledge of fundamentals of numerical methods used for modeling and simulation of complex phenomena described by ordinary and partial differential equations. The following topics are covered: finite-difference approximation of derivatives; interpolation; integration; steady-state boundary value problems; local and global errors; stability, consistency, and convergence; matrix equations and iterative methods; initial value problems for ordinary differential equations; Runge-Kutta methods; multi-step methods; absolute stability; stiff ODE; numerical solution of PDEs; parabolic problems; hyperbolic problems; method of lines; von Neumann analysis; operator splitting; introduction to spectral approximation.

The course involves hands-on experience with programming (in Matlab or Python) and solving problems on computers. Solid knowledge of undergraduate mathematics including basic understanding of the theory of ordinary and partial differential equations of physics and engineering as well as basic programming skills are required.

 

Computational Fluid Dynamics (6 ECTS)

Fluid flows are ubiquitous in engineering. Fluid mechanics provides the theoretical foundation to a broad spectrum of engineering applications that range from tiny laboratory-on-a-chip devices to the largest thermal and hydroelectric power plants. The rich dynamics of fluid motion leads to numerous effects that engineers may wish to exploit or suppress. Mathematical description of fluid flows most commonly involves non-linear partial differential equations that make analytical solution impossible or impractical. Therefore, approximate solution using numerical methods has been widely implemented since the advent of digital computers. Nowadays, the Computational Fluid Dynamics (CFD) is a well-established discipline. CFD is widely used in science and engineering alike. It accelerates optimal design and offers important insights in the flow dynamics.

The course will introduce the students to important theoretical and practical aspects of the CFD. It will explain how to describe the fluid flow by partial differential equations with suitable initial and boundary conditions, and how to transform those equations into computer algorithms. A brief overview of general-purpose numerical methods will be provided, with comments on their relevance to the CFD. Then, specialized methods for different types of flows will be introduced. This will be followed by a brief discussion of the advanced topics of fluid-structure interaction, turbulence modelling and high-performance computing. Computer practice classes will allow the students to acquire basic skills of programming simple methods from scratch, get acquainted with existing CFD software packages, develop intuition for distinguishing physical effects from numerical artifacts, and learn to use the CFD wisely.