Aslan Kasimov
Project Center for Energy Transition and ESG
Prof. Aslan Kasimov is the director of the Master’s program on Applied Computational Mechanics and a member of the Skoltech Center for Energy Transition.
His research is in the area of theoretical and computational fluid dynamics, in particular analysis of the dynamics of detonation waves and other reacting flows.
Prof. Kasimov holds a Ph.D. degree in Theoretical and Applied Mechanics from the University of Illinois at Urbana-Champaign, received in 2004. His undergraduate education was received from Moscow Engineering-Physics Institute (MEPhI), which he graduated in 1993 with a degree in chemical physics. Prior to joining Skoltech, Prof. Kasimov was a lecturer and instructor in applied mathematics at the Department of Mathematics of MIT (2005-2009), served as a founding faculty member at the King Abdullah University of Science and Technology (KAUST, 2009-2016), and held a researcher position in the Tamm Theoretical Physics Department at the Lebedev Physical Institute of the Russian Academy of Sciences.
He was a recipient of a US AFOSR Young Investigator Award in 2007 for his work on detonation theory and of a number of graduate awards at the University of Illinois. He has substantial teaching and advising experience at both graduate and undergraduate levels at MIT, KAUST, and Skoltech. At KAUST, he helped establish a vigorous graduate program in Applied Mathematics and Computational Science, where he created and taught original courses on applied partial differential equations, stability and bifurcation theory, asymptotic analysis, and theoretical fluid dynamics. Many graduates of the program continued as doctoral students or postdocs at various universities around the world including Stanford University, UC Berkeley, Oxford University, MIT.
More in CV.
Positions as interns, MSc, or PhD students are open – see below under News tab.
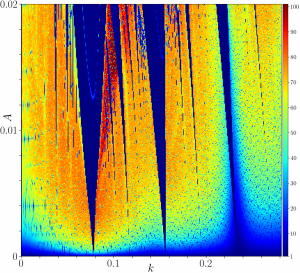
Prof. Kasimov’s research is focused on the theory and numerical simulation of reacting flows, multiphase flows, and other nonlinear systems that exhibit complex, often chaotic, dynamics. Much of his past research has been on the theory of detonations, with particular emphasis on the analysis of stability of detonation waves and on the construction of asymptotic models of multi-dimensional detonations. He has also made contributions to various other areas of nonlinear science, such as: traffic modeling, co-authoring a theory of jamitons; theory of water waves, especially involving hydraulic jumps; pattern-forming instabilities in reaction-diffusion equations in biology; dispersive waves, such as those arising in the complex Gross-Pitaevskii equation; analysis of partial differential equations. Since joining Skoltech in 2018, Prof. Kasimov’s research focused on the analysis and computation of complex fluid flows and of phase-transition phenomena occurring in additive manufacturing processes. Presently, he is a member of the Center for Energy Transition, and his research focus is on problems of detonation theory and computation, in particular concerning the problem of detonation in nonuniform media and of deflagration-to-detonation transition.Research highlight: Arnold tongues arising in the problem of detonation propagation in periodically nonuniform media.
|
- A. Yu. Goldin, Sh. M. Magomedov, L. M. Faria, and A. R. Kasimov, Study of a qualitative model for combustion waves: flames, detonations, and deflagration-to-detonation transition. Computers and Fluids, (2024). https://doi.org/10.1016/j.compfluid.2024.106213
- Sh. Aamir, A. R. Kasimov, Application of the Fourier Neural Operator to the reactive Burgers equation of detonation theory (submitted, 2023)
- A. Yu. Goldin, A. R. Kasimov, Detonation cell locking in periodically nonuniform mixtures (submitted, 2023)
- A. Yu. Goldin, T. O. Medvedeva, and A. R. Kasimov, Mode locking in gaseous detonation propagation in a channel with periodically varying friction. Physics of Fluids, 34(9), 096104 (2022). https://doi.org/10.1063/5.0103370
- A. Yu. Goldin, A. R. Kasimov, Synchronization of detonations: the Arnold tongues and devils staircases. Journal of Fluid Mechanics, 946, R1, (2022). https://doi.org/10.1017/jfm.2022.581
- A. R. Kasimov and A. Yu. Goldin. Resonance and mode locking in gaseous detonation propagation in a periodically nonuniform medium. Shock Waves (2021): 31, 841-849, https://doi.org/10.1007/s00193-021-01049-z
- E. L. Sharaborin, O. A. Rogozin, and A. R. Kasimov. Computational Study of the Dynamics of the Taylor Bubble. Fluids 6.11 (2021): 389. https://doi.org/10.3390/fluids6110389
- E. L. Sharaborin, O. A. Rogozin, and A. R. Kasimov. The Coupled Volume of Fluid and Brinkman Penalization Methods for Simulation of Incompressible Multiphase Flows. Fluids, 2021, 6, 334, https://doi.org/10.3390/fluids6090334
- P. N. Krivosheyev, A. O. Novitski, K. L. Sevrouk, O. G. Penyazkov, I. I. But, A. R. Kasimov, Experimental and numerical investigation of gaseous detonation in a narrow channel with obstacles. Fluids 2021, 6, 224. https://doi.org/10.3390/fluids6060224
- A. R. Kasimov and A. R. Gonchar. Reactive Burgers model for detonation propagation in a non-uniform medium, Proceedings of the Combustion Institute. (2020) https://doi.org/10.1016/j.proci.2020.07.149
- D. I. Kabanov, A. R. Kasimov, A minimal hyperbolic system for unstable shock waves, Communications in Nonlinear Science and Numerical Simulation, 70, 282-301, 2019 (https://doi.org/10.1016/j.cnsns.2018.10.022); preprint: http://arxiv.org/abs/1807.05403
- D. I. Kabanov, A. R. Kasimov, Linear stability analysis of detonations via numerical computation and dynamic mode decomposition, Physics of Fluids, 30, 036103, 2018 (https://dx.doi.org/10.1063/1.5020558); preprint: http://arxiv.org/abs/1712.03276
- A. Sow, R. Semenko, and A.R. Kasimov, On a stabilization mechanism for low-velocity detonations, Journal of Fluid Mechanics, 816, 539–553, 2017 (https://dx.doi.org/10.1017/jfm.2017.70)
- R. Semenko, L. Faria, A. Kasimov, B. Ermolaev, Set-valued solutions for non-ideal detonation, Shock Waves, 26(2), 141–160, 2016 (http://dx.doi.org/10.1007/s00193-015-0610-3); preprint: http://arxiv.org/abs/1312.2180)
- L. Faria, A. Kasimov, R. R. Rosales, Study of a model equation in detonation theory: multidimensional effects, SIAM Journal on Applied Mathematics, 76(3), 887–909, 2016 (https://dx.doi.org/10.1137/15M1039663).
- A. R. Kasimov, R. E. Semenko, On modeling gaseous detonation in porous media by the one-dimensional reactive Euler equations, Gorenie i Vzryv (Moskva) – Combustion and Explosion, 9(4), 19–26, 2016.
- L. Faria, A. Kasimov, R. R. Rosales, Theory of weakly nonlinear self-sustained detonations, Journal of Fluid Mechanics, 784, 163–198, 2015 (https://dx.doi.org/10.1017/jfm.2015.577)
- L. Faria, A. Kasimov, Qualitative modeling of the dynamics of detonations with losses, Proceedings of the Combustion Institute, 35(2), 2015–2023, 2015 (http://dx.doi.org/10.1016/j.proci.2014.07.006) preprint: http://arxiv.org/abs/1407.8475
- J. Sierra, A. Kasimov, P. Markowich, R.-M. Weish ̈aupl, On the Gross-Pitaevskii equation with pumping and decay: stationary states and their stability, Journal of Nonlinear Science, 25(3), 709–739, 2015 (https://dx.doi.org/10.1007/s00332-015-9239-8) preprint: http://arxiv.org/abs/1310.2388
- A. Kasimov, Detonation analogs revisited, Proceedings of 25th ICDERS, Leeds, UK, 2015. (http://www.icders.org/ICDERS2015/abstracts/ICDERS2015-312.pdf)
- L. Faria, A. Kasimov, R. R. Rosales, A toy model for multi-dimensional cellular detonations, Proceedings of 25th ICDERS, Leeds, UK, 2015(http://www.icders.org/ICDERS2015/abstracts/ICDERS2015-294.pdf)
- L. Faria, A. Kasimov, R. R. Rosales, Weakly nonlinear dissipative detonations, Proceedings of 25thICDERS, Leeds, UK, 2015 (http://www.icders.org/ICDERS2015/abstracts/ICDERS2015-296.pdf)
- A. Kasimov and S. Korneev, Detonation in supersonic radial outflow, Journal of Fluid Mechanics, 760, 313-341, 2014 (https://dx.doi.org/10.1017/jfm.2014.598)(highlighted on the journal cover).
- L. Faria, A. Kasimov, R. R. Rosales, Study of a model equation in detonation theory, SIAM Journal on Applied Mathematics, 74(2), 547-570, 2014 (https://dx.doi.org/10.1137/130938232)
- L. M. Faria, A. R. Kasimov, R. R. Rosales, From Zeldovich–von Neumann–Doering model to theories of pulsating and cellular detonations, Proceedings of the 3rd International Conference on Combustion and Detonation “Zel’dovich Memorial”, Moscow, Russia, 2014
- A. R. Kasimov, S. Korneev, Detonation in supersonic radial outflow, Proceedings of the 21stInternational Conference on Nonlinear Problems of Hydrodynamic Stability and Turbulence, Moscow State University, Russia, 2014
- R. Parshad, M. Beauregard, A. Kasimov, B. Said-Houari, Global existence and finite-time blowup in a class of stochastic nonlinear wave equations, Communications in Stochastic Analysis, 8(3), 381-411, 2014
- R. Parshad, N. Kumari, A. Kasimov, H. Ait Abderrhamane, Turing patterns and long-time behavior in a three-species food-chain model, Mathematical Biosciences, 254, 83-102, 2014
- A. Kasimov, R. Racke, B. Said-Houari, Global existence and decay of solutions of the Cauchy problem in thermoelasticity with second sound, Applicable Analysis, 93(5), 2014
- B. Said-Houari, A. Kasimov, Damping by heat conduction in the Timoshenko system: Fourier and Cattaneo are the same, Journal of Differential Equations, 255(4), 611-632, 2013
- A. Kasimov, L. Faria, R. R. Rosales, Model for shock wave chaos, Physical Review Letters, 110, 104104, 2013 (https://dx.doi.org/10.1103/PhysRevLett.110.104104) (preprint:http://arxiv.org/abs/1202.2989)
- B. Seibold, M. Flynn, A. Kasimov, R. Rosales, Constructing set-valued fundamental diagrams from jamiton solutions in second order traffic models, Networks and Heterogeneous Media, 8(3), 745-772, 2013
- B. Said-Houari, A. Kasimov, Decay property of Timoshenko system in thermoelasticity, Mathematical Methods in Applied Sciences, 35, 314-333, 2012
- M. R. Flynn, A. R. Kasimov, J.-C. Nave, R.R. Rosales, B. Seibold, Self-sustained nonlinear waves in traffic flow, Physical Review E 79, 056113, 2009
- B. Taylor, A. R. Kasimov, D.S. Stewart, Mode selection in weakly unstable two-dimensional detonations, Combustion Theory and Modelling, 13:6, 973-992, 2009
- M. R. Flynn, A. R. Kasimov, J.-C. Nave, R. R. Rosales, B. Seibold, On jamitons, self-sustained nonlinear traffic waves, arXiv:0809.2828v2, 2008
- A. R. Kasimov, A stationary circular hydraulic jump, the limits of its existence and its gasdynamic analogue, Journal of Fluid Mechanics, 601, 189-198, 2008
- D. S. Stewart and A. R. Kasimov, State of detonation stability theory and its application to propulsion, Journal of Propulsion and Power, 22, No. 6, 1230-1244, 2006
- D. S. Stewart and A. R. Kasimov, Theory of detonation with an embedded sonic locus, SIAM Journal on Applied Mathematics, 66, No. 2, 384-407, 2005
- A. R. Kasimov and D. S. Stewart, Asymptotic theory of evolution and failure of self-sustained detonations, Journal of Fluid Mechanics, 525, 161-192, 2005
- A. R. Kasimov and D. S. Stewart, On the dynamics of self-sustained detonations: A numerical study in the shock-attached frame, Physics of Fluids, 16(10), 3566-3578, 2004
- A. R. Kasimov and D. S. Stewart, Theory of detonation initiation and comparison with experiment, TAM Report 1035, Theoretical & Applied Mechanics, UIUC, 2004
- A. R. Kasimov and D. S. Stewart, Spinning instability of gaseous detonations, Journal of Fluid Mechanics, 466, 179-203, 2002
- A.A. Borisov, O.I. Mel’nichuk, A.R. Kasimov, B.A. Khasainov, K.Ya. Troshin, and V. Kosenkov, On the energy evolution in gaseous detonation waves, Journal de Physique IV, C4, Vol. 5, 1995
- Young Investigator Program Award, US Air Force Oce of Scientific Research, 2007-2009
I am looking for ambitious students as either short-term interns or MSc students or PhD students to join a research group in fluid dynamics. The group is engaged in theoretical and computational research on the analysis of complex flows in reacting and multiphase systems. Particular directions of current interest are:
- analysis of compressible reacting flows, including multiphase flows
- development of high-order numerical algorithms for simulation of fluid flows with shock waves and other sharp interfaces
- development and application of machine learning techniques to the simulation of reacting flows
Positions require strong background and passionate interest in physics/mechanics and applied and computational mathematics .
Skoltech offers excellent conditions for work and study including state-of-the-art experimental and computational facilities and internationally competitive stipends and salaries.
Interested candidates are welcome to write to Prof. Aslan Kasimov at for further details.
- Andrei Goldin, PhD student (MSc in Mechanics and Mathematics, Novosibirsk State University)
- Shamil Magomedov, PhD student (MSc in Mechanics and Mathematics, Moscow State University)
- Vignesh Kumar, PhD student (MSc, Skoltech)
- Mariush Soroka, MSc student (BSc, Belarusian State University, Minsk)
- Tenzin Tadin, MSc student (MSc, Phystech)
- Ksenia Lapshova, MSc student (BSc, Bauman Moscow State Technical University)
- Fedor Belolutski, MSc student (BSc, Moscow Engineering Physics Institute)
- Danis Gatiatov
- Tatiana Medvedeva
- Ivan But
- Shahzeb Aamir
- Bintang Alam Semesta WAM
- Vignesh Kumar
- Vladimir Fanaskov (MSc, Physics, Moscow State University)
- Evgenii Sharaborin (MSc, Phystech)
- Diana Gazizova (MSc in Mechanics and Mathematics, Moscow State University)
Former research interns:
- Andrei Gonchar (MIPT)
- Diana Gazizova (MSU, Mechanics and Mathematics)
- Olesya Schendrigina (MSU, Mechanics and Mathematics)
- Shamil Magomedov (MSU, Mechanics and Mathematics)
- Margarita Selezneva (MSU, Mechanics and Mathematics)
- Albina Khabibulina (MSU, Mechanics and Mathematics)
Courses in the ACM program:
- Numerical Methods for Conservation Laws (6 credits, Terms 3-4, Feb-May 2024, syllabus)
- Fundamentals of Fluid Mechanics (3 credits, Term 4, Apr-May 2024, syllabus to appear)
- Advanced Fluid Mechanics: Compressible Flows (3 credits, Term 5, Sep-Oct 2024, syllabus to appear)
- Modeling with Open-Source Software (3 credits, Term 6, Nov-Dec 2024, syllabus to appear))
Other teaching at Skoltech:
Mathematical Methods in Engineering and Applied Science (6 credits, since 2019)
This is a course primarily aimed at first year Masters students in engineering and applied sciences. It introduces essential mathematical techniques used in solving various applied problems. The topics include: methods of applied linear algebra, statistical methods, data analysis, optimization, basic applied ordinary and partial differential equations.
Numerical Methods in Engineering and Applied Science (6 credits) (2019-2021)
The course is intended to provide the understanding and working knowledge of numerical methods required for modeling and simulation of complex phenomena. It focuses on fundamentals of the methods such as accuracy, stability, convergence, and consistency rather than learning how to use canned computer codes. The course involves first-hand experience with programming and solving real problems on computers. Solid knowledge of calculus, linear algebra, complex variables is essential, and basic understanding of the theory of ordinary and partial differential equations of physics and engineering as well as basic programming skills are required. The following topics will be covered: solving nonlinear equations, matrix equations, eigenvalue problems, interpolation, numerical differentiation and integration, numerical solution of ordinary and partial differential equations, optimization problems, and data analysis.
- Статья в naked-science.ru о языках Арнольда в теории детонации: Физики нашли способ упорядочить взрыв
- Phys.org: Physicists find way to control detonation wave in promising new type of engine.
Профессор Аслан Рамазанович Касимов получил ученую степень PhD в теоретической и прикладной механике в Университете штата Иллинойс в Урбана-Шампейн, США, в 2004 году. Он является выпускником кафедры физики быстропротекающих процессов Московского инженерно-физического института (МИФИ) 1993 года. До прихода в «Сколтех» профессор Касимов работал преподавателем прикладной математики на факультете математики Массачусетского технологического института (2005-2009), был профессором-основателем университета науки и технологии им. Короля Абдуллы (KAUST, 2009-2016), также работал сотрудником в отделении теоретической физики им. И.Е. Тамма в Физическом институте им. П.Н. Лебедева РАН.
Он был лауреатом премии и гранта US AFOSR Young Investigator Award в 2007 году за работу по теории детонации. Имеет значительный опыт преподавания и руководства аспирантами в Массачусетском технологическом институте и KAUST. В KAUST он был одним из основателей программы магистратуры и аспирантуры по прикладной математике и вычислительной науке, где он создал и преподавал оригинальные курсы по прикладным уравнениям в частных производных, теории устойчивости и бифуркаций, асимптотическому анализу и теоретической гидродинамике.